금일 유투브 You can't bounce a ball under a table 앞부분을 보고 생각해본 해당 상황에 대한 물리학이 가미된 intuition적 고찰
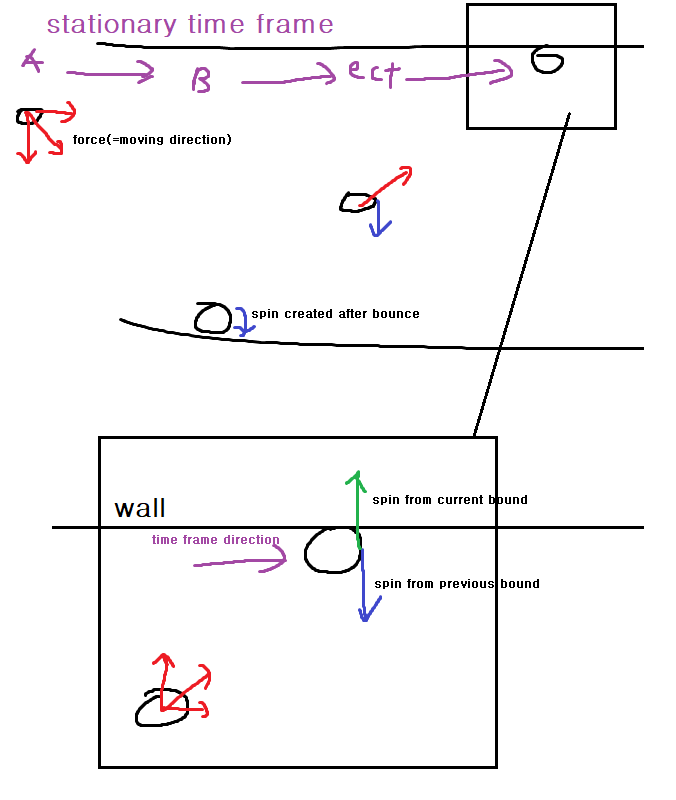
그렇다면 결론은 결국 1st 스핀과 2nd 스핀과의 싸움이라고 볼 수 있고
그렇다면 이 1st 스핀과 2nd 스핀의 회전의 에너지가 어떻게 걸리는지가 핵심이다.
이 스핀운동의 핵심은 운동하는 물체와 정지한 물체 사이의 마찰을 통한 운동에너지의 일부 또는 전부가 회전에너지로 변환하는것이고 따라서 이를 생각해 볼 때 공이 2nd bounce 지점에서 앞으로 가냐 뒤로 되튕기냐를 결정하는 스핀 에너지의 비교는 다시 말하자면
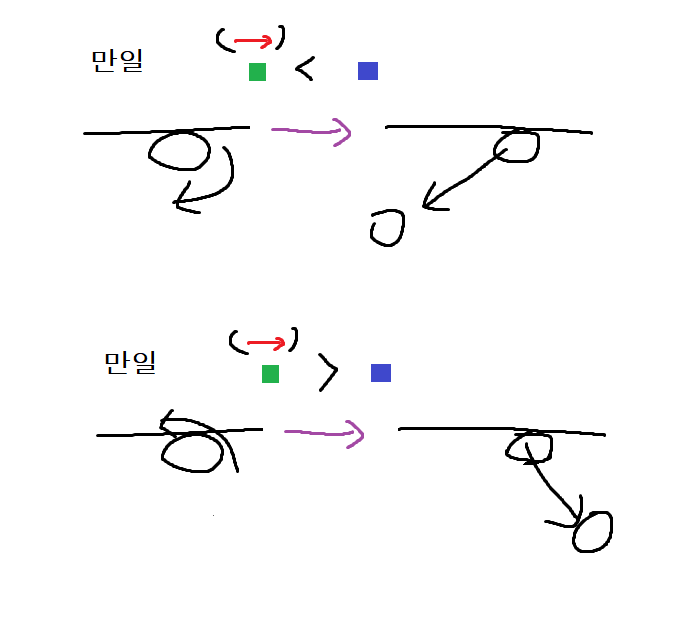
(1st bound 앞쪽 성분 운동 에너지*마찰계수등스핀으로의변환계수0~1) >부등호 비교< (2nd bound 앞쪽 성분 운동 에너지* 마찰계수등스핀으로의변환계수0~1)
이다.
이 비교 부등호 앞뒤 각 요소들을 보자면
1.앞쪽 성분 운동에너지
분명히 초기 공이 가진 운동 에너지는 상식적으로 최초가 제일 크며 주위 매질을 뚫으며 이동할수록 감소 할 것이다. 따라서 핵심은 1st bound와 2nd bound 사이를 이동할 때 얼마나 매질 등 환경에 의해 공의 운동에너지가 감소하냐가 키 포인트이다. 하지만 여기서는 일반 공기 사이에서 그 감소가 무의미하게 작다고 본다.
2. 마찰계수등스핀으로의변환계수
운동에너지의 얼마가 회전으로 변환되는가가 핵심이다. 그런데 위 아래 벽은 당연하게 같은 재질이기 때문에 이의 마찰계수는 같다. 그런데 여기서 단순하게 마찰계수라고 쓰지 않고 변환계수라고 쓴 것에는 이유가 있고 이를 알아차려야 한다.
아무리 나처럼 물리시간에 잠을 잤다고 해도 마찰식에 중력이 들어갔다는것은 알 수 있을 것이며 최소한 모터로 돌아가는 바퀴를 방 바닥에 가져다 댔을때와 온 힘을 다해 꾹 눌렀을 때 둘 중 어느 상황에서 바닥이 더 뜨거워지는지는 현대인이라면 머리속에서 시뮬레이션이 가능하다.
그렇다면 1st bounce에서는 공이 위에서 아래로 튀겨졌으므로 접촉면을 향한 힘이 중력의 도움으로 초기 발사시보다 더 클 것이고 따라서 이에 의한 마찰력도 더 쌔져서 최종 변환계수도 더 클 것이다.
2nd bounce를 보면 1st bounce에서 튀긴 공이 아래서 위로 중력을 역행하며 에너지를 잃고 천장으로 튀긴다. 따라서 전문적인 물리용어를 쓰면 수직항력이 더 작아져서 결과적으로 마찰력도 더 작아 변환계수도 더 작아질 것이다.
이를 줄이면 명백하다.
위 아래 막힌 공간에서 튀겨서 공을 통과시키기 위해서는 공을 아래로 집어 던질 때 앞으로 가는 힘을 일정 이상 강하게 줘서 회전반발을 무시할 정도의 힘 이상을 주던지
아니면 단순하게 그냥 위로 집어던지면 된다.
정말 간단하다.
그냥 단순히 '공을 아래로 집어던지지 않고 위로 집어던지면 된다'가 답이다.
이를 가지고 12분 53초짜리 영상을 줄줄히 만들면서 제목을 넌 이것을 할 수 없다는 자극적인 제목을 달고 공을 아래로만 집어던지며 자기의 이전 영상에 대한 말과 3D 시뮬레이션만 줄줄히 늘어놓다 외부에서 수주받은 광고를 달고 영상이 끝난다.
예전에는 TV가 바보상자였고 유투브가 개인 취미 영상 공간이였다면
현재는 유투브가 바로 그 바보상자이다.
그냥 시간을 멍하게 보내려는 사람이 아니라면 이를 적절히 파악하는 것이 현대인의 기본소양이다.